 |
Estás leyendo parte de la revista de Noviembre de 1960
|
Recomienda este artículo a un amigo
|
|
 |
 HACE
ALGUNOS DIAS, me dijo un amigo: "No me explico la forma en que los
hombres de ciencia averiguan la distancia a la Luna o al Sol. y cuando mencionan
las galaxias, ¿cómo pueden saber dónde se hallan? ¿Han
usado los astrónomos una cinta de medir para saberlo?
No me extraña su desconfianza; pero el hecho es que no siempre hay
necesidad de medir distancias en la forma que se emplea con una mesa o un
cuarto. Existen otros métodos, que son tan buenos y aún mejores.
En primer lugar, la distancia a la Luna se puede medir enviando ondas de
radio y registrando el tiempo que invierten en retornar hasta la Tierra.
 En
una de la pruebas verificadas, el tiempo total de ida y regreso fué
de 2,4 segundos. Esto significa, por supuesto, que las ondas de radio tardaron
1,2 segundos desde la Tierra hasta la Luna. Como quiera que se propagan
a razón de 300.000 k.p.s., la Luna se hallaba a 300.000 X 1,2, o
sea a 360.000 kilómetros de distancia. Es difícil que alguien
se animase a comprar una cinta de esa longitud, e irla desenvolviendo a
medida que viajaba hasta la Luna, a través del espacio.
Igual sistema se ha empleado para medir la distancia al planeta Venus, y
también al Sol. Se podría suponer que dado que el Sol es un
cuerpo gaseoso, no refleja las ondas de radio; pero lo cierto es que lo
hace. Las ondas de radio rebotan de llamas, ciclones, zonas cargadas de
electricidad y gases.
El método con ondas de radio -o radar, si se prefiere denominarlo-
no da buenos resultados con los planetas más distantes. No contamos
todavía con transmisores de radar suficientemente poderosos para
enviar un haz potente que pueda llegar al planeta Plutón, por ejemplo.
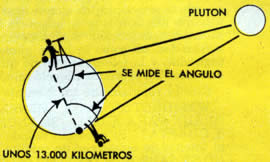
En este caso, se usa el siguiente método: desde dos puntos de la
Tierra, lo más separados que sea posible, se enfocan telescopios
sobre Plutón, y se registran los ángulos respectivos.
Se obtienen, así, los datos necesarios. Se cuenta con un triángulo
en que se conocen un lado -de 13.000 kilómetros, por ejemplo- y dos
ángulos. Es muy simple calcular el largo de los otros dos lados.
Se halla, en esta forma, que Plutón está a 5.800.000.000 de
kilómetros.
Cuando se trata de medir la distancia a las estrellas, nuestra mayor línea
de base (el diámetro en el Ecuador tiene 12.756 kilómetros)
es muy pequeña. Todos sabemos lo que pasa cuando se trata de usar
este método para medir grandes distancias empleando una línea
de base relativamente pequeña. Los ángulos son casi de 90°,
y el error más insignificante en la medida de éstos, producirá
una dimensión totalmente equivocada en los dos lados largos del triángulo.
La forma de solucionar este problema es utilizando una línea de base
más larga. ¿Existe alguna que sea mayor que el diámetro
de la Tierra?
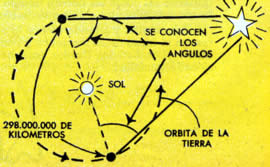 Por
supuesto que existe. Es el diámetro de la órbita de nuestro
planeta alrededor del Sol. En este caso, un astrónomo dirige una
noche una visual a una estrella, y, seis meses más tarde,
repite la operación y consigue, así, los dos ángulos
necesarios. La base del triángulo tiene 2 x 149 millones de kilómetros,
o sean 298.000.000 de kilómetros.
Gracias a este método, se sabe que la estrella más cercana
se encuentra a unos 39 billones de kilómetros (39 seguido de 12 ceros).
Sea dicho de paso, la luz recorre en un año -a 300.000 kilómetros
por segundo- una distancia de unos 9 billones y medio de kilómetros.
Por lo tanto, podemos decir que la estrella más cercana está
a 4 "años de luz" de distancia.
Pero este método en que se emplea el diámetro de la órbita
como línea de base, sólo es conveniente hasta distancias de
unos 100 años de luz. A partir de esto, se comienzan a obtener nuevamente
ángulos de casi 90 grados, por lo cual los triángulos resultan
irresolubles.
Afortunadamente, existe la forma de transponer el obstáculo.
En nuestro próximo número trataremos del problema de medir
distancias realmente GRANDES. ¿Sabe usted cuál es la mayor
distancia que se ha medido? Se ha captado el choque de dos galaxias situadas
a una distancia de unos 6.000.000.000 de años de luz. Para averiguar
el número de kilómetros, debemos multiplicar 6.000.000.000
por 9.463.000.000.000, cuyo producto es 56.778.000.000.000.000.000.000,
¿Se animaría usted a medir esta distancia con una cinta? |
Fuente: Revista Mecánica Popular - Volumen 27 -
Noviembre 1960 - Número 5
|
|
|
